Последовательность чисел Фибоначчи

Уровни фибоначчи – один из базовых инструментов анализа движений в контексте их размеров. На первый взгляд может показаться, что это значения, которые просто за уши притянуты к реальности, однако можно просто открыть любой график и посмотреть на соотношения между разными колебаниями. Тут даже самые упёртые скептики сдадутся. Этот необычный метод активно используется во многих стратегиях, а также играет важную роль при волновой разметке движений, Эллиотт уделял большое внимание пропорциям, что позволяет в значительной степени повысить точность таких прогнозов. На данный момент уровни фибоначчи входят в состав базовых графических инструментов практически любого терминала, и даже если он отсутствует, его легко можно найти в интернете или, на крайний случай, посчитать самому на калькуляторе.

В основе значений фибоначчи лежит числовая последовательность, которая имеет такое же название. Это достаточно простой алгоритм, последовательность строится по следующему принципу: каждый последующий член последовательности фибоначчи равен сумме двух предыдущих. Начинается она с нуля и двух единиц. Впрочем, ноль очень часто опускается.

 

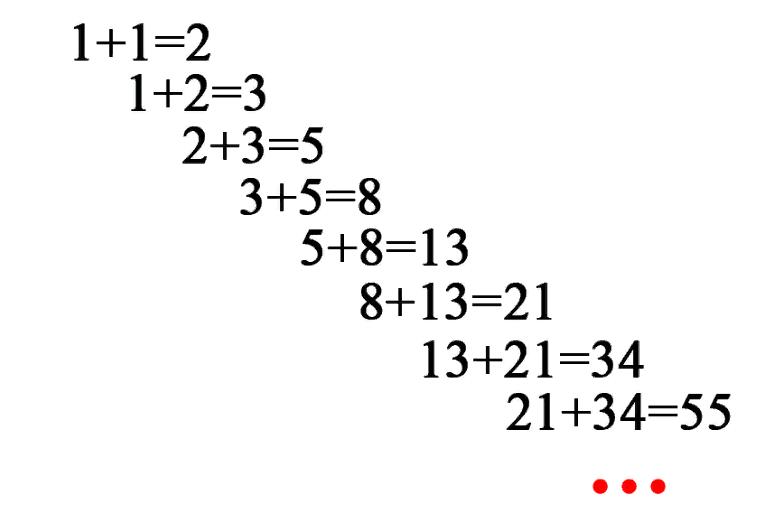
По мере продолжения этой последовательности каждый предыдущий член будет всё больше приближаться к так называемому “Золотому сечению”. В процентном выражении это 61,8%. Взято это значение из простой формулы деления отрезка на две части так, чтобы меньшая часть относилась к большей так же, как большая часть относится ко всему отрезку. После несложных расчётов получается как раз 61,8%. Так мы получаем самое главное значение, от которого строятся все остальные. Второе важное значение – 38,2%. Оно получается путём вычета из 100% значения основного.  Рассмотрим, как это получается:

 

Интерес представляет правый столбик, показанный на картинке. Буквально десятый член последовательности уже показывает очень близкие к нашему золотому сечению значения. Далее, продолжая строить ряд, мы получаем ещё более точные. В целом, в трейдинге вполне достаточно использовать общепринятое значение 61,8%, дальнейшее уточнение уже ни к чему.

Важность последовательности фибоначчи

Теперь перейдём к более важному вопросу, а именно по какой причине всё это работает. Дело в том, что золотое сечение названо так совсем не случайно. Первые упоминания датируются аж четвёртым веком до нашей эры в работах известного математика Евклида, который упоминал золотое сечение в контексте построения пятиугольника.  Само же название связывают обычно с очень известным инженером, художником и изобретателем – да Винчи, хотя именно литературное распространение началось с математических пособий Германии, где другой известнейший учёный Ом ввёл его именно в этой формулировке. В целом, всё это не так важно, главное – это идея, которая лежит в самом соотношении. К которому приводит последовательность фибоначчи. Подобное соотношение можно встретить в следующих областях:

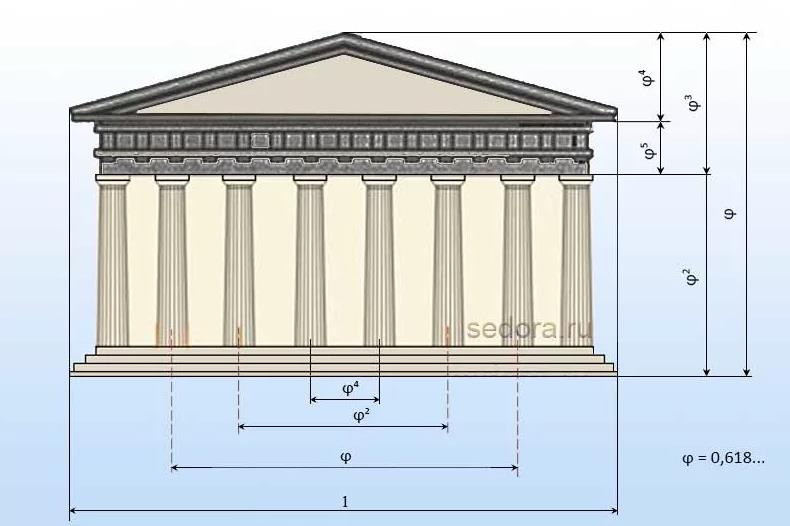
1. Архитектура. История знает огромное количество примеров, где было сознательно использовано правило разделения различных элементов исходя из их соотношений между собой определённым коэффициентом. Самый яркий пример – пирамиды в Египте, а также многие здания (храмы) в Древней Греции. Прямоугольник, разделённый таким образом получается очень гармоничным, поэтому он часто лоижлся в основу формы здания. То же самое относится и к элементам украшения, декора, везде можно проследить эту туенденцию. Конечно же, это не говорит о том, что прямо вот вся архитектура была заточена именно под такие пропорции, но тот факт, что они далеко нередко появлялись, свидетельствует о том, что золотое сечение было известно давно, и использовалось вполне сознательно. В целом, и последовательность фибоначчи появилась не просто так – числа, которые приближаются к золотому сечению позволяют определить само сечение через такую математическую операцию, как вычисление предела.

2. Геометрия молекул и химия. Очень сложные формы соединений на атомном уровне могут содержать как числа, входящие в последовательность фибоначчи, так и само золотое сечение. Как уже говорилось ранее, наш коэффициент присутствует в пятиугольнике, а сами атомы между собой образуют очень сложные геометрические фигуры. В основном, коэффициент прослеживается в додекаэдрах и икосаэдрах. Не вдаваясь в подробности, это многогранные фигуры, имеющие сложную симметрию. Также здесь присутствует число из поселдовательности фибоначчи – 21, которое получается одной молекулой, вокруг которой располагается ещё двадцать молекул. В итоге вся эта композиция из двадцати одной молекулы даёт додекаэдр.

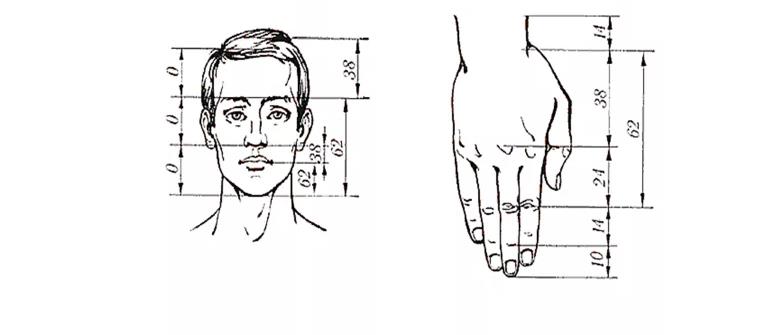
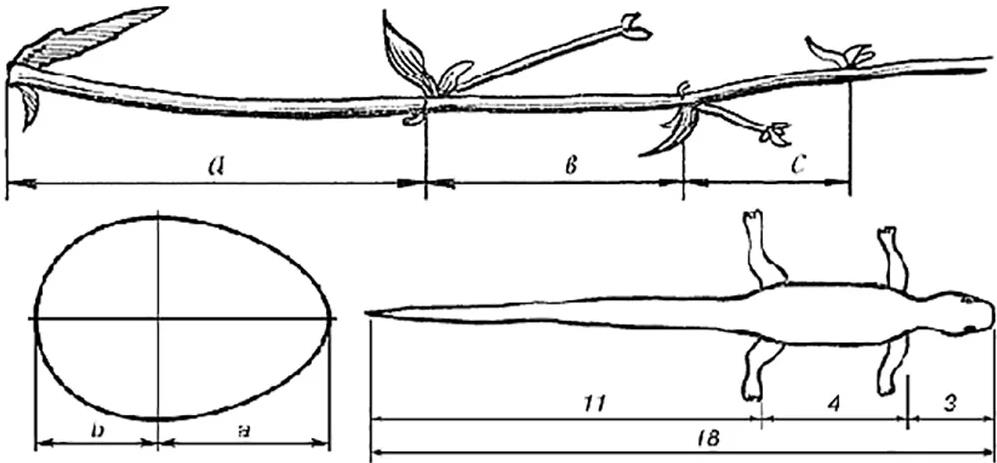
3. Биология. Пропорции тела очень приближены к главному коэффициенту.  Например, соотношение между расстояние от подбородка до бровей стремится к коэффициенту, входящему в последовательность чисел фибоначчи, по отношению оставшейся части головы, то есть лба. Аналогичная ситуация и с размером ладони, только в роли этого сечения выступает линия, проходящая через сустав между третьей и второй фалангой. Также считается, что изначально на подобные части, как в последовательности фибоначчи, делил тело пупок. Однако, со временем начались отклонения от этих значений, что объясняется эволюцией и приспособлением под окружающие человека условия.

 

4. Музыка. Здесь речь идёт о количество нот разной длины. Например, золотое сечение использовал Иоганн Себастьян Бах, один из величайших композиторов в истории.

5. Природа. Золотое сечение прослеживается в цветах, листьях, расположении сучков на более крупном суке дерева. Наибольший интерес представляет раковина улитки, которая “раскручивается” по строгой спирали, шаг которой определяется нашим коэффициентом. Вообще, если взглянуть на все примеры, становится очевидным, что каким-то необъяснимым образом и сама природа стремится к таким пропорциям. Человеческое восприятие объектов, в которых есть такие соотношения ассоциируется с гармонией, что довольно странно на фоне восприятия симметричных объектов, как практически идеальных. Тем не менее, данный факт известен очень давно и активно применяется.

 

Данное соотношение, полученное из чисел фибоначчи, ложится в основу системы коэффициентов, которые называются уровнями фибоначчи. Они устанавливают пропорции между двумя разнонаправленными движениями, по ним можно определять размеры коррекции и предполагать точки окончания. Но об этом мы поговорим позднее, а сейчас перейдём непосредственно к самим числам фибоначчи, а вернее, последовательности, которая имеет очень важное значение в волновой теории, разработанной Эллиоттом.

Последовательность чисел фибоначчи в волновой теории

До этого мы говорили о предельном отношении двух соседних членов последовательности чисел фибоначчи. Теперь посмотрим, как волновая теория использует последовательность. Из общего описания нам известно, что все движения делятся на импульсы и коррекции. В глобальном масштабе вся волновая конструкция стремится к циклу роста и снижения, меняется размерность, но эти две фазы последовательно происходят одна за другой. Минимальный набор волн для отличия одной структуры от другой – 5 и 3. У импульсов пять составляющих, у коррекции – три. В этом мы видим первые два числа, которые относятся к последовательности фибоначчи. И даже суперцикл из двух фаз также входит в последовательность – это 1 и 1. Рассмотрим более подробно рост и коррекцию.

1. В составе импульса мы можем выделить 5 элементов – три из них также импульсы, оставшиеся два – коррекции. Соответственно, при таком приближении у нас уже получается 5+3+5+3+5=21 Итого двадцать одна волна составляет импульс.
2. Коррекция, как известно, состоит из трёх движений, в которых два – импульсы и одно – коррекция. При таком раскладе у нас получается 5+3+5=13 волн. Здесь есть исключение, так как иногда первая волна в коррекции может быть представлена тройкой, но зато это компенсируется тем, что вторая волна может быть треугольником, в котором не 3, а уже 5 волн. К тому же треугольники могут встречаться и в четвёртой волне импульса.

 

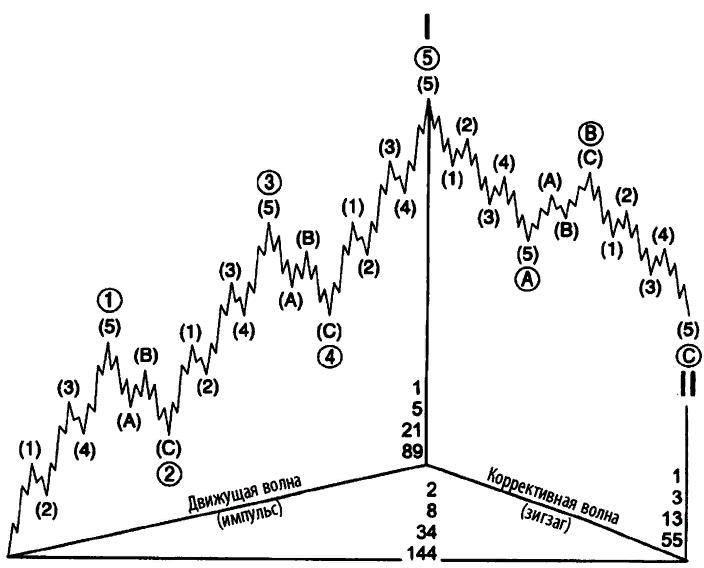
Что мы видим в итоге: 21 волна в импульсе и 13 волн в коррекции в рамках одного цикла. Оба числа из последовательности фибоначчи, причём следуют они сразу за 8 и 5 волн из предыдущего примера. И если это покажется совпадением, перейдём ещё на один уровень подробнее. В этом случае получается следующее:

1. Импульс представлен 21 волной, коррекция 13, значит, весь импульс будет состоять из 21+13+21+13+21=89 волн. Это также вытекает из структуры простого 5+3.
2. Коррекция состоит из:  21+13+21=55 волн.

И снова у нас два числа из последовательности фибоначчи. В сумме такой цикл даёт следующее число – 144. Так можно продолжить до бесконечности, и каждый раз будем получать следующие два числа из последовательности фибоначчи. Подобная последовательность свидетельствует о том, что волновая теория имеет глубокую связь с происходящим на рынке, ведь мы имеем не только количество волн, но и самое главное соотношение и его производные, которые также вписываются в гармонию природы и поведения людей. И чем больше объёмы, тем чётче должна прослеживаться зависимость всего происходящего в разных циклах между собой.  Это выражается как в самой структуре, так и в коэффициентах.

 

Читайте далее - Уровни Фибоначчи